MAGNITUDES PROPORCIONALES

Dos magnitudes son proporcionales cuando al variar una, también lo hace la otra es la misma proporción. La proporcionalidad puede ser inversa o directa.

PROPORCIONALIDAD DIRECTA: Dos magnitudes son directamente proporcionales cuando al aumentar una, también aumenta la otra ó cuando al disminuir una, también disminuye a la otra. Matemáticamente esto puede representarse como:
$$y=kx$$
Aquí, "x" recibe el nombre de variable independiente, "y" el nombre de variable dependiente y "k" es la constante de proporcionalidad. Esto se lee: "y es directamente proporcional a x". 

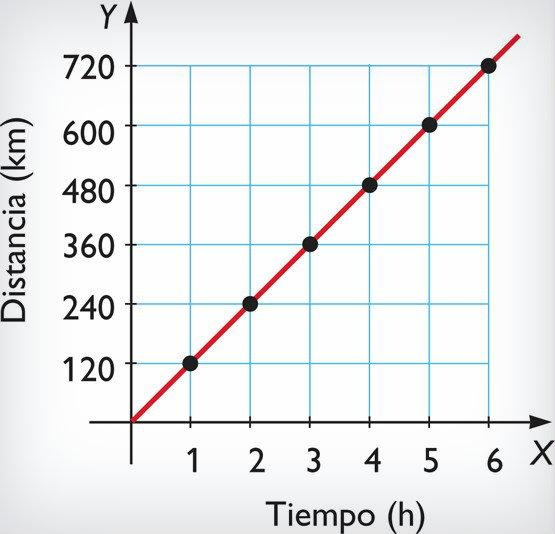
Geométricamente esta relación se representa por una línea recta. 

PROPORCIONALIDAD INVERSA: Dos magnitudes son inversamente proporcionales cuando al aumentar una, disminuye la otra ó cuando al disminuir una, aumenta la otra. Nótese que la diferencia entre ambos tipos de proporcionalidad es la forma en como varían las cantidades. Esta proporcionalidad se representa como:

$$y=\frac{k}{x}$$

Esto se lee "y es inversamente proporcional a x". Geométricamente esta relación representa una curva. 

PROBLEMAS RESUELTOS

1. El cuadrado de A varía proporcionalmente al cubo de B; si A=3, B=4. Determinar el valor de B cuando $A=\frac{\sqrt{3}}{3}$. 

Solución: En los problemas de magnitudes proporcionales, generalmente lo primero que debe hacerse es calcular la constante de proporcionalidad con los primeros datos que se nos brindan. El problema nos dice que las magnitudes varían proporcionalmente, por tanto se trata de una variación directamente proporcional. Podemos plantear:
$$A^{2}=k \cdot B^{3}$$
Sustituyendo los primeros  datos, determinamos el valor de k.
$$3^2=k \cdot 4^3$$
$$9=k \cdot 64 \rightarrow k=\frac{9}{64}$$
Una vez encontrado el valor de la constante k, cualquier valor de A o B puede determinarse conociendo uno de ellos. Para este problema nos piden determinar B para cuando $A=\frac{\sqrt{3}}{3}$. Sustituyendo datos:
$$\left(\frac{\sqrt{3}}{3}\right)^2=\frac{9}{64} \cdot B^3$$
$$\frac{3}{9}=\frac{9}{64} \cdot B^3 \rightarrow B^3=\frac{3}{9} \cdot \frac{64}{9}$$
Como B está elevado al cubo, se extrae raíz cúbica a ambos miembros (operador inverso), por tanto queda:
$$\sqrt[3]{B^3}=\sqrt[3]{\frac{192}{81}}$$
$$B=\frac{4}{3}$$

2. La frecuencia de una onda de radio es inversamente proporcional a la longitud de onda. Si una onda de 250 m de longitud tiene una frecuencia de 1200 kilociclos por segundo, ¿Cuál es la longitud de una onda que tiene una frecuencia de 800 kilociclos por segundo?

Solución: De nuestras clases de física conocemos que la frecuencia se representa por "f" y la longitud de onda por Lambda $(\lambda)$. Del enunciado podemos plantear que:
$$f=\frac{k}{\lambda}$$
Sabemos que lo primero a calcular, es la constante de proporcionalidad. Sustituyendo los datos conocidos:
$$1200=\frac{k}{250} \rightarrow k=1200 \cdot 250 =300,000$$
Ahora tendríamos que despejar $\lambda$, ya conocido el valor de k podemos plantear:
$$\lambda = \frac{300,000}{800}=375\ m$$

3. Dividir 1400 en tres partes directamente proporcionales a 4, 6 y 10 e inversamente proporcionales a 8, 4 y 2. Indicar la diferencia entre la mayor y la menor de las partes. 

Solución: Como vamos a repartir proporcionalmente a 3 cantidades, tendremos que plantear 3 relaciones de proporcionalidad para ambos casos (directo e inverso).

Reparto directo: como aquí las cantidades son proporcionales a 4, 6 y 10 podemos plantear:
$$x=4k$$
$$y=6k$$
$$z=10k$$
Tomando en cuenta que la suma de estas cantidades tiene que ser igual al total, escribimos:
$$x+y+z=1400 \rightarrow 4k+6k+10k=1400$$
$$20k=1400 \rightarrow k=\frac{1400}{20}=70$$
Por tanto, las cantidades repartidas directamente proporcionalmente son:
$$x=4(70)=280$$
$$y=6(70)=420$$
$$z=10(70)=700$$
Ahora nos toca determinar las cantidades cuando el reparto es inverso, para ello planteamos:
$$a=\frac{k_1}{8}$$
$$b=\frac{k_1}{4}$$
$$c=\frac{k_1}{2}$$
De igual manera, la suma de estas cantidades debe ser igual al total, es decir:
$$a+b+c=1400$$
$$\frac{k_1}{8}+\frac{k_1}{4}+\frac{k_1}{2}=1400 \rightarrow  \frac{7}{8}{k_1}=1400$$
Despejando ${k_1}$ se obtiene:
$$k_{1}=1600$$
Por tanto las cantidades repartidas inversamente proporcional son:
$$a=\frac{1600}{8}=200$$
$$b=\frac{1600}{4}=400$$
$$c=\frac{1600}{2}=800$$
Vemos que la cantidad mayor de los dos repartos es 800 y la menor 200, por tanto la diferencia es 600.

PROBLEMAS PROPUESTOS

1. Se ha descubierto que la cantidad de trabajo hecho por un hombre es una hora varía en razón directa de su salario por hora e inversamente proporcional a la raíz cuadrada del número de horas que trabaja por día. Si puede terminar una pieza en 6 días cuando trabaja nueve horas diarias a un dólar por hora. ¿Cuántos días tardará en terminar la misma pieza cuando trabaja 16 horas diarias a un dólar y medio por hora?

RPTA: 5.75 días

2. El valor de un diamante varía proporcionalmente al cuadrado de su peso. Si la piedra que se compró a 640,000 soles, se rompe en dos piezas, de las cuales una es los tres quinto de la otra. ¿Cuánto será la pérdida en porcentaje sufrida por romperse el diamante. 

RPTA: 46.875%

3. ¿Cuántos gramos tiene una esmeralda que vale 112,500 soles, si una de 6 gramos vale 7,200 soles? Se sabe que el precio es proporcional al cubo del peso. 

RPTA: 15 gramos

4. Determinar la profundidad de un pozo sabiendo que una piedra tarda un segundo y 4/10 en llegar al fondo. Se sabe que un cuerpo que cae libremente recorre una distancia que es proporcional al cuadrado del tiempo y que una piedra recorre 19.60 metros en 2 segundos. 

RPTA: 9.064 metros

5. Se reparte N directamente proporcional a 1, 8 y 1/2N. Si a 1 le corresponde 1/2. Calcular N. 

RPTA: 6